Understanding Binary Numbering
All computers function using a system of switches that can be in one of two positions, on or off. This is called a binary system, with “off” being represented by the digit 0 and “on” being represented by the digit 1. A binary number will include only the digits 0 and 1. Network device addresses also use this binary system to define their location on the network. The IP address is based on a dotted decimal notation of a binary number. You must have a basic understanding of the mathematical properties of a binary system to understand networking. The following sections describe the mathematics involved in the binary numbering system and explain how to convert a decimal (base 10) number to a binary (base 2) number and vice versa.
Decimal and Binary Systems
The decimal (base 10) system is the numbering system used in everyday mathematics, and the binary (base 2) system is the foundation of computer operations. In the decimal system, the digits are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. When quantities higher than 9 are required, the decimal system begins with 10 and continues all the way to 99. Then the decimal system begins again with 100, and so on, with each column to the left raising the exponent by 1.
The binary system uses only the digits 0 and 1. Therefore, the first digit is 0, followed by 1. If a quantity higher than 1 is required, the binary system goes to 10, followed by 11. The binary system continues with 100, 101, 110, 111, 1000, and so on. Table 4-1 shows the binary equivalents of the decimal numbers 0 through 19.
Table 4-1 Decimal Versus Binary Numbers
| Decimal Number | Binary Number |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
| 17 | 10001 |
| 18 | 10010 |
| 19 | 10011 |
Least Significant Bit and Most Significant Bit
Most people are accustomed to the decimal numbering system. While the base number is important in any numbering system, it is the position of a digit that confers value. The number 10 is represented by a 1 in the tens position and a 0 in the ones position. The number 100 is represented by a 1 in the hundreds position, a 0 in the tens position, and a 0 in the ones position.
In a binary number, the digit on the rightmost side is the least significant bit (LSB), and the digit on the leftmost side is the most significant bit (MSB). The significance of any digits in between these sides is based on their proximity to either the LSB or the MSB. Figure 4-7 shows the relationships of bit significance to the values for base 10 and base 2 numbering systems.
Figure 4-7 Bit Significance
Base-10 Decimal Conversion – 63204829
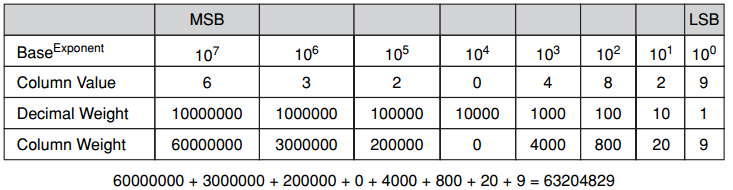
Base-2 Binary Conversion – 1110100 (233)

Base 2 Conversion System
Understanding the base 2 system is important because an IP version 4 (IPv4) address consists of 32 binary bits. Each digit is 1 bit. The 32 bits are divided into four sets of 8 bits, called octets. A dot (period) is placed between each set to separate them. (A byte is another name for 8 bits; however, for the purposes of this module, 8 bits will be referred to as an octet.)
The various classes of addresses are based on the octet boundaries, so it is helpful to get used to such groupings. It is also an ease-of-use issue, because 8-bit binary numbers are easier to convert than 32-bit binary numbers. When converting a binary IP address, you only convert one octet at a time. The highest possible binary octet is 11111111, which converts to the decimal number 255. The lowest possible binary octet is 00000000, which is the decimal number 0. That means that with 8 bits, you can have 256 different number combinations, 0 to 255 inclusive.
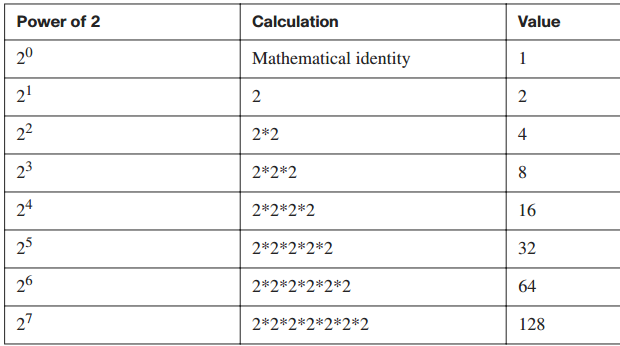
Powers of 2
To understand how binary numbers are used in IP addressing, you must understand the mathematical process of converting a decimal number to a binary number and vice versa. Calculator batteries run down and charts can be misplaced, but if you know the mathematical principles, a piece of paper and pencil are all that you need to convert binary numbers to decimal numbers and to convert decimal numbers to binary numbers. There are charts available to help with decimal-to-binary conversion, showing, for example, 20 = decimal 1, 21 = decimal 2, 22 = decimal 4, and so on. Table 4-2 illustrates which decimal numbers are produced for powers of 2.
Decimal-to-Binary Conversion
Decimal numbers can be converted to binary numbers through a specific process, as shown in Figure 4-8.
Figure 4-8 Decimal-to-Binary Conversion

This example shows a simple binary conversion of the decimal number 35. The base exponent line shows base 2 numbers and their exponents (2 * 2 = 4 * 2 = 8, and so on). The decimal value of the base exponent number is listed in the second row, and the binary number is displayed in the third row. The table describes the steps to determine the binary number. Notice that the first 2 bits of the binary number are 0s; these are known as leading 0s. In reality, the decimal number 35 would only be a 6-bit binary number. Because IP addresses are laid out as four sets of octets, the binary number is made into an octet by placing 0s to the left of the 6-bit number.
The steps used in converting the number 35 to a binary number are as follows:
Step 1 Looking at Figure 4-8, what is the greatest power of 2 that is less than or equal to 35? 128 does not go into 35, so place a 0 in that column.
Step 2 64 does not go into 35, so place a 0 in that column.
Step 3 25 (32) is smaller than 35. 32 goes into 35 one time. Place a 1 in that column.
Step 4 Calculate how much is left over by subtracting 32 from 35. The result is 3.
Step 5 Check to see whether 16 (the next lower power of 2) fits into 3. Because
it does not, a 0 is placed in that column.
Step 6 The value of the next number is 8, which is larger than 3, so a 0 is placed in that column, too.
Step 7 The next value is 4, which is still larger than 3, so it too receives a 0.
Step 8 The next value is 2, which is smaller than 3. Because 2 fits into 3 one time, place a 1 in that column.
Step 9 Subtract 2 from 3, and the result is 1.
Step 10 The decimal value of the last bit is 1, which fits in the remaining number. Therefore, place a 1 in the last column. The binary equivalent of the decimal number 35 is 00100011.
Binary-to-Decimal Conversion
As with decimal-to-binary conversion, there is usually more than one way to convert binary numbers to decimal numbers. You can convert binary numbers to decimal numbers using the positional values based on the powers of 2 and identifying the columns with nonzero values, which contribute to the final numerical value. Figure 4-9 illustrates this process.
Figure 4-9 Binary-to-Decimal Conversion
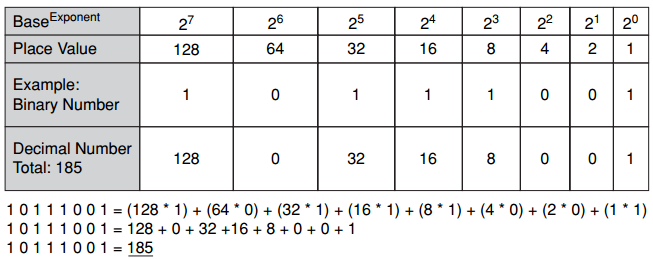
The steps used for converting the binary number 10111001 to a decimal number are as follows:
Step 1 Find the place value that corresponds to any 1 bit in the binary number, according to its position. For example, as shown in Figure 4-9, the binary bit in the 27 column is 1, so the decimal total is 128.
Step 2 There is a 0 in the 26 (64) column. The decimal equation is 128 + 0 = 128.
Step 3 There is now a 1 in the 25 (32) column. The decimal equation becomes 128 + 32 = 160.
Step 4 There is a 1 in the 24 (16) column. Adding the value to the decimal total gives 160 + 16 = 176.
Step 5 The next column, 23, has a 1, so add the value 8 to the decimal total, giving 176 + 8 = 184.
Step 6 There are 0s in the 22 and 21 columns. Add 0s to the decimal total: 184 + 0 + 0 = 184.
Step 7 Finally, there is a 1 in the 20 (1) column. Now, add 1 to 184. The result is 185. The decimal equivalent of the binary number 10111001 is 185.